A. Determinan Metode Sarrus
Ciri khas metode ini adalah pola perkalian menyilang elemen matriks.
Ciri khas ini juga dimiliki pola Sarrus 4×4, hanya saja dengan jumlah pola yang lebih banyak yaitu 3 pola.
 B. Determinan Matriks 3×3 Metode Ekspansi Kofaktor
B. Determinan Matriks 3×3 Metode Ekspansi Kofaktor
Walaupun konsep dasar minor dan kofaktor sama, akan tetapi terdapat perbedaan penggunaan minor dan kofaktor dalam menghitung determinan dan invers matriks 3×3.
Dalam determinan, minor-kofaktor yang dihitung hanya terbatas pada baris atau kolom tertentu saja dan biasa disebut ekspansi baris dan ekspansi kolom.
Sedangkan dalam invers, kita harus menghitung sembilan elemen minor dan kofaktor sampai diperoleh matriks baru yaitu matriks minor dan matriks kofaktor.
Minor
Definisi minor adalah determinan submatriks persegi setelah salah satu baris dan kolomnya dihilangkan.
Minor dilambangkan dengan “Mij” dimana “i” sebagai baris dan “j” sebagai kolom matriks yang dihilangkan.
Baris dan kolom dihilangkan bukan berarti dibuang, akan tetapi baris dan kolom tersebut hanya tidak diikutsertakan dalam submatriks yang baru.
Submatriks artinya bagian kecil dari matriks, sedangkan matriks persegi adalah matriks yang mempunyai jumlah baris sama dengan jumlah kolom atau sebut saja berordo nxn. Misalnya matriks persegi 3×3 maka submatriksnya berordo 2×2.
Jadi, menghitung minor matriks 3×3 adalah menghitung determinan submatriks 2×2.
Contoh: M12 = baris ke-1 dan kolom ke-2 dihilangkan
| Matriks | Submatriks | Minor |
Contoh: M23 = baris ke-2 dan kolom ke-3 dihilangkan
| Matriks | Submatriks | Minor |
Kofaktor
Dalam kofaktor, elemen minor matriks dapat bernilai positif dan negatif. Kofaktor dilambangkan dengan “Cij” dan dapat dihitung dengan rumus:
Contoh:
| Kofaktor (C11) | Kofaktor (C12) | Kofaktor (C13) |
Cara mudah untuk mengetahui nilai kofaktor, yaitu:
| Jika i + j = bilangan genap maka kofaktor bernilai positif |
| Dan jika i + j = bilangan ganjil maka kofaktor bernilai negatif |
Sebenarnya tanpa menghitung satu persatu kita bisa dengan mudah mengetahui tanda kofaktor matriks. Caranya cukup tuliskan tanda positif dan negatif secara bergantian di depan lambang minor.
Seperti yang saya tulis sebelumnya bahwa terdapat perbedaan cara menghitung determinan dan invers matriks 3×3.
Oleh karena itu, untuk selanjutnya pembahasan minor-kofaktor dalam invers bisa dibaca dalam invers matriks ordo 3×3.
Sedangkan pembahasan ini berlanjut ke determinan metode ekspansi kofaktor yaitu ekspansi baris dan kolom.
>Ekspansi Baris
Ekspansi baris dimulai dari setiap elemen kolom pertama atau elemen dengan nilai j = 1 (ai1) dan arahnya bergerak secara mendatar sepanjang jumlah kolom matriks.
Rumus umum determinan ekspansi baris:
Kenapa tandanya + (plus) semua?
Karena tanda plus atau minus ditentukan oleh kofaktor dan ekspansi baris mana yang digunakan.
Jika ekspansi baris ganjil misalnya ekspansi baris pertama dan baris ketiga, maka tandanya dimulai dengan positif.
Dan jika ekspansi baris genap seperti ekspansi baris kedua dan baris keempat, maka rumusnya dimulai dengan tanda negatif.
Dan hal yang hampir sama juga berlaku pada rumus umum ekspansi kolom.
Jadi, berdasarkan pola rumus umum tersebut dapat ditentukan tiga rumus determinan ekspansi baris matriks 3×3, yaitu:
Ekspansi baris pertama

Ekspansi baris kedua

Ekspansi baris ketiga

Meskipun mudah namun tanda kofaktor justru yang paling sering menjadi penyebab kesalahan menghitung determinan. Jadi, telitilah dalam menuliskan rumus ekspansi!
Sifat-sifat determinan :
1. Determinan suatu matriks sama dengan determinan dari transposnya.
2. Penambahan atau pengurangan suatu kelipatan bukan nol tidak akan mempunyai pengaruh pada determinan.
3. Jika semua elemen dari suatu baris atau kolom adalah nol, determinan adalah nol.
C. Invers
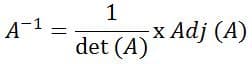


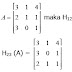


Tidak ada komentar:
Posting Komentar