Turunan Fungsi (1 Variabel)

A. Pengertian Turunan

Turunan adalah pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai yang dimasukan, atau secara umum turunan menunjukkan bagaimana suatu besaran berubah akibat perubahan besaran lainnya. Proses dalam menemukan turunan disebut diferensiasi.

Pada fungsi y = f(x), turunan dari variabel y terhadap variabel x dinotasikan dengan  atau 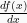  atau y’ dan didefinisikan sebagai:

B. Aturan menentukan turunan fungsi

Turunan bisa kita tentukan tanpa adanya proses limit.

Untuk kebutuhan ini dirancang teorema atau pernyataan mengenai turunan dasar, turunan dari operasi aljabar pada dua fungsi, aturan rantai untuk turunan fungsi komposisi, dan juga turunan fungsi invers.

C. Turunan dasar

Beberapa aturan dalam turunan fungsi antara lain:

1. f(x), menjadi f'(x) = 0
2. Jika f(x) = x, maka f’(x) = 1
3. Aturan pangkat berlaku jika f(x) = xn, maka f’(x) = n X n – 1
4. Aturan kelipatan konstanta berlaku jika (kf) (x) = k. f’(x)
5. Aturan rantai berlaku jika ( f o g ) (x) = f’ (g (x)). g’(x))

D.Turunan jumlah, selisih, hasil kali, serta hasil bagi dua fungsi

Contohnya fungsi f dan g terdiferensialkan pada selang I, maka fungsi f + g, f – g, fg, f/g, ( g (x) ≠ 0 pada I ) terdiferensialkan pada I dengan aturan sebagai berikut:

1. ( f + g )’ (x) = f’ (x) + g’ (x)
2. ( f – g )’ (x) = f’ (x) – g’ (x)
3. (fg)’ (x) = f’(x) g(x) + g’(x) f(x)
4. ((f)/g )’ (x) = (g(x) f’ (x)- f(x) g’ (x))/((g(x)2)

E. Turunan fungsi trigonometri

1. d/dx ( sin x ) = cos x
2. d/dx ( cos x ) = – sin x
3. d/dx ( tan x ) = sec2 x
4. d/dx ( cot x ) = – csc2 x
5. d/dx ( sec x ) = sec x tan x
6. d/dx ( csc x ) = -csc x cot x

F. Turunan fungsi invers

(f-1)(y) = 1/(f’ (x)), atau dy/dx 1/(dx/dy)

G. Rumus Dasar Turunan dari Turunan Fungsi

Beberapa aturan yang ada di dalam turunan fungsi antara lain:

1. f(x), menjadi f'(x) = 0
2. Jika f(x) = x, maka f’(x) = 1
3. Aturan pangkat berlaku jika f(x) = xn, maka f’(x) = n X n – 1
4. Aturan kelipatan konstanta berlaku jika (kf) (x) = k. f’(x)
5. Aturan rantai berlaku jika ( f o g ) (x) = f’ (g (x)). g’(x))

H. Rumus-rumus Turunan Fungsi AlJabar

1. Rumus Turunan Fungsi Pangkat

Turunan Fungsi berbentuk pangkat, turunannya bisa memakai rumus: sebagai berikut:

Sehingga, rumus turunan fungsi pangkatnya adalah:

2.  Rumus turunan hasil kali fungsi 

Rumusan Fungsi f(x) turunan yang terbentuk dari perkalian fungsi u(x) dan v(x), adalah sebagai berikut:

Sehingga, rumus turunan fungsinya yaitu:

f'(x) = u’v +uv’

3. Rumus turunan fungsi pembagian 

Sehingga, rumus turunan fungsinya yaitu:

4. Rumus turunan pangkat dari fungsi

 

Perlu diingat, jika f(x) = xn , maka dari itu:

Sehingga, rumus turunan fungsinya yaitu:

f'(x) = nu(n – 1) . u’

5. Rumus-rumus Turunan Trigonometri

Berdasarkan definisi dari turunan, maka bisa kita dapatkan beberapa rumus turunan trigonometri yaitu sebagai berikut: (dengan u dan v masing-masing fungsi dari x), antara lain: y’ =

1. y = sin x→ y’ = cos x
2. y = cos x → y’ = -sin x
3. y = tan x → y’ = sec2 x
4. y = cot x → y’ =  -csc2 x
5. y = sec x → y’
6. y = csc x → y’ = csc × cot x
7. y = sinn  xy’ = n sinn-1 × cos x
8. y = cosn  x → y’ = -n cosn-1 × sin x
9. y = sin u → y’ = u’ cos u
10. y = cos u → y’ = u’ sin u
11. y = tan u → y’ = ui sec2 u
12. y = cot u → y’ = -u’ csc2 u
13. y = sec u → y’ = u’ sec u tan u
14. y = csc u → y’ = u’ csc u cot u
15. y = sinn  u → y’ = n.u’ sinn-1 cos u
16. y = cosn u → y’ = -n.u’  cosn-1 . sin u

I. Turunan Fungsi Aljabar

*Definisi Turunan

Turunan fungsi f(x) terhadap x didefinisikan oleh:

dengan syarat limitnya ada.

*Notasi Turunan

Turunan pertama fungsi y = f(x) pada x bisa kita notasikan seperti berikut ini:

• y’ = f’x ⇒ lagrange
•  ⇒ leibniz
• Dxy = Dx[f(x)]⇒ euler

Dari definisi di atas bisa kita turunkan beberapa rumus turunan seperti di bawah ini:

1. f(x) = k  ⇒  f ‘(x) = 0
2. f(x) = k x  ⇒  f ‘(x) = k
3. f(x) = xn ⇒ f ‘(x) = nxn-1
4. f(x) = k u(x)  ⇒ f ‘(x) = k u'(x)
5. f(x) = u(x) ± v(x)  ⇒ f ‘(x) = u'(x) ± v'(x)

dengan k = konstan

Perhatikan beberapa contoh berikut ini:

1. f(x) = 5  ⇒  f ‘(x) = 0
2. f(x) = 2x  ⇒  f ‘(x) = 2
3. f(x) = x2 ⇒  f ‘(x) = 2x2-1 = 2x
4. y = 2x4  ⇒  y’ = 2. 4x4-1 = 8x3
5. y = 2x4 + x2 − 2x  ⇒  y’ = 8x3 + 2x − 2

Untuk mencari turunan dari fungsi yang memuat bentuk akar atau pecahan, langkah pertama yang harus kita lakukan yaitu merubah terlebih dahulu fungsi tersebut ke dalam bentuk pangkat (eksponen).

Berikut terdapat beberapa sifat akar dan pangkat yang sering dipakai, atara lain:

• xm . xn = xm+n
• xm/xn = xm-n
• 1/xn = x-n
• √x = x1/2
• n√xm = xm/n