Matriks adalah susunan bilangan-bilangan rill atau kompleks yang diatur dalam baris-baris dan kolom-kolom berbentuk persegi panjang.
Contoh mudah matriks dapat kamu lihat dalam ilustrasi di bawah ini:

Ilustrasi di atas dapat kamu baca seperti ini: a11 dibaca baris ke-1 dan kolom ke-1; a12 dibaca baris ke-1 dan kolom ke-2; atau amn yang berarti baris ke-m dan kolom ke-n. Banyaknya baris dan kolom dalam matriks disebut dengan ordo. Urutan yang perlu diingat adalah baris kemudian kolom. Matriks dalam ilustrasi di bawah ini memiliki ordo 2x3, karena memiliki dua baris dan tiga kolom.
B. Jenis-jenis Matriks
Matriks memilik banyak jenis yang dapat dibedakan dengan ordo dan elemen-elemennya. Jenis matriks adalah sebagai berikut.
1. Matriks baris.
Matriks yang terdiri dari satu baris. Contoh :

2. Matriks kolom.
Matriks yang terdiri dari satu kolom. Contoh :

3. Matriks persegi.
Matriks yang banyak baris sama dengan banyak kolom. Contoh :

4. Matriks nol.
Matriks yang semua elemennya nol. Contoh :

5. Matriks identitas.
Matriks yang elemen diagonal utamanya sama dengan 1, sedangkan elemen-elemen lainnya sama dengan 0. Contoh :

6. Matriks Skalar.
Matriks yang elemen diagonal utamanya sama, sedangkan elemen di luar elemen diagonalnya bernilai nol. Contoh :

7. Matriks diagonal.
Matriks persegi memiliki elemen di luar diagonal utama yang bernilai nol. Contoh :

8. Matriks segitiga atas.
Matriks persegi yang elemen diagonal bawah bernilai nol. Contoh :

9. Matriks segitiga bawah.
Matriks persegi yang elemen diagonal atas bernilai nol. Contoh :

10. Transpos matriks A atau (A t).
Matriks yang disusun dengan cara menuliskan baris ke-i matriks A menjadi kolom ke-i dan sebaliknya, menuliskan kolom ke-j matriks A menjadi baris ke-j
Misalnya, jika matriks A

maka matriks transpos dari A adalah :

C. Operasi pada matriks
Penjumlahan Matriks
Operasi hitung matriks pada penjumlahan memiliki syarat yang harus dipenuhi agar dua buah matriks dapay dijumlahkan. Syarat dari dua buah matriks atau lebih dapat dijumlahkan jika memiliki nilai ordo yang sama. Artinya, semua matriks yang dijumlahkan harus memiliki jumlah baris dan kolom yang sama.
Matriks dengan jumlah baris 3 dan kolom 4 hanya bisa dijumlahkan dengan matriks dengan jumlah baris 3 dan kolom 4. Matriks dengan jumlah baris 3 dan kolom 4 tidak bisa dijumlahkan dengan matriks dengan jumlah baris 4 dan kolom 3. Kesimpulannya, jumlah baris dan kolom antar dua matriks yang akan dijumlahkan harus sama.
Contoh cara melakukan operasi penjumlahan pada matriks:
Pengurangan Matriks
Seperti halnya operasi hitung penjumlahan matriks, syarat agar dapat mengurangkan elemen-elemen antar matriks adalah matriks harus memiliki nilai ordo yang sama. Cara melakukan operasi pengurangan pada matriks dapat dilihat seperti cara di bawah.
Contoh cara melakukan operasi pengurangan pada matriks:
Perkalian Matriks
Pembahasan operasi hitung matriks selanjutnya yang akan dibahas adalah perkalian matriks. Perkalian matriks yang akan dibahas di bawah adalah perkalian matriks dengan skalar dan perkalian matriks dengan matriks. Selengkapnya simak operasi hitung perkalian matriks di bawah.
Perkalian Matriks dengan Skalar
Cara melakukan operasi skalar pada matriks adalah dengan mengalikan semua elemen-elemen matriks dengan skalarnya. Jika k adalah suatu konstanta dan A adalah matriks, maka cara melakukan operasi perkalian skalar dapat dilihat melalui cara di bawah.
Operasi Perkalian Dua Matriks
Seperti yang telah disinggung sebelumnya, syarat dua buah matriks dapat dikalikan jika memiliki jumlah kolom matriks pertama yang sama dengan jumlah baris matriks ke dua. Ordo matriks hasil perkalian dua matriks adalah jumlah baris pertama dikali jumlah kolom ke dua.
Matriks A memiliki jumlah kolom sebanyak m dan jumlah baris r, matriks B memiliki jumlah kolom sebanyak r dan jumlah baris m, hasil perkalian matriks A dan B adalah matriks C dengan jumlah kolom m dan jumlah baris n.
Perkalian dua matriks  dapat diperoleh dengan cara di bawah.
dapat diperoleh dengan cara di bawah.

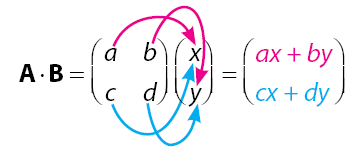


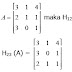


Tidak ada komentar:
Posting Komentar